Options Mentoring

[wayneL]

Ahem.....er, well I'm not really comfortable with that term. But this is a follow on from Tech/A's expertise thread, where there was a lot of interest in options.

Some of us here have some experience....so lets just say "sharing what we know".

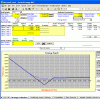
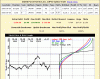
Firstly, options are a vastly complex subject. What I know has been slowly added to over the last few years and I don't think it is something that can be absorbed quickly...at least not for us booze addled old farts.

That complexity is what makes them so useful...yet dangerous.

Useful, because you can construct a situation to take advantage of whatever view of the market you have. Indeed , you must have a view of where the market is headed, even if that view is merely "somewhere" or "nowhere".

Dangerous, because of the leverage and strange price behaviour (strange if you have not studied enough). Options have so many "gotchas" it's mind boggling and you are trading against the smartest ****holes in the universe, bar none...the market makers!

They do not have to be dangerous though, they can also be the most effective risk control tool.

It's a bit like handleing stallions. They have the wherewithall to rip your head off your shoulders, and in the wrong hands they have done just that. In the right hands they are your best friend and a joy to be with. Just never take your eye off them LOL

 

[wayneL]

A couple of free resources:

1/ If you click on my website link below, there is a free download for Charles Cottle's book "Coulda Woulda Shoulda". Charles has been a US options market maker for 25 odd years. It's a hard read, but in my opinion its the best book available.

Might be a bit advanced for some, so beginners should start with one the books by Bower or Tate or similar.

Try to get a solid grasp of the Greeks. Ignorance of these will be at you peril. Some of the seminar wombats are teaching that all this does not matter. Ther students wonder how there bought call option is in loss when the stock is up....hmmm go figure.

Any questions on the greeks are most welcome, I'll try and confuse you even more...er, less...or sumthin'

2/ http://www.hoadley.net/options/strategymodel.htm This is a free strategy modeller which will give you payoff diagrams and you can play with different strikes, expiries, etc example as below.

 

[wayneL]

US market vs Aussie market

Apart from far greater choice and liquidity, the US market has two great avantages.

1/ Cost - brokerage is much cheaper

2/ You can trade ANY position online...any spread you can dream up, naked calls...anything.

Enouigh for now, avagoodweegend

P.S. This is not a monopoly, so join in all you options guys

 

[DTM]

Thanks for the information Wayne. I have three questions:

1. Could you give us the effects of the greeks

2. What the market makers do and how they can affect the market ie by moving the market and their pricing models via greeks.

3. Some basic strategies you would use with different situations

Thanks in advance.

Have a good weekend too.

 

[tech/a]

Thanks Wayne looking forward to some good discussion.

Perhaps a glossary of terms would be an idea as they come up
coupled with a fairly concise explaination.

Wonder if Joe can have a
single screen that can be added to as a term pops up rather than a thread which would have a glossary all over the place.

Thanks again---where would you like the banana's delivered?? (hahaha)

 

[Joe Blow]

Wonder if Joe can have a
single screen that can be added to as a term pops up rather than a thread which would have a glossary all over the place.

Tech, I'll see what I can do.

 

[doctorj]

Perhaps we should set up a trading/investment Wiki to cover all related subjects including options. See http://wikipedia.org/ for an example. It's format is probably better suited to the task than using a forum as it links questions with answers more effectively and makes searching more efficient.

 

[positivecashflow]

Option Greeks:


Theta: Change in the price of an option with respect to a change in its time to expiration (time value).

Vega: Change in the price of an option with respect to its change in volatility

Delta: Change in the price of an option relative to the change of the underlying security.

Gamma: Change in the delta of an option with respect to the change in price of its underlying security.

Rho:
Rho is the change in option price given a one percentage point change in the risk-free interest rate.

ASX Link to explain greeks in more detail:

http://www.asx.com.au/investor/options/greeks.htm

 

[positivecashflow]

Example of Greeks for a trade:

 

[wayneL]

Yes the greeks are where we should start and the definitions are all over the internet. The ASX definitions that Pos posted are, in my view both overly simplified and overly technical. I could never understand the standard definitions in a practical sense.

I hope to define them, and use examples in more understandable language...a tall order.

I also like to lump in Implied Volatility with the greeks even though, strictly, it is not one of them.

Rho we can safely disregard in a stable interest rate environment...but be sure to fill in the correct risk free rate in your strategy modeller....5.75% I believe...close enough!

I like to separate them into two groups 1/ delta and gamma 2/ theta, implied volatility(IV) and vega (also known as omega)

 

[wayneL]

Lets see if I can cut through the confusion....

Delta:

As Pos posted - Change in the price of an option relative to the change of the underlying security.

Lets suppose we own some at the money call options in Delta Omega Gold LTD (DOG). The price we payed doesn't matter for the purpose of this example.

So lets say DOG moves up 15c during the days trading, but we notice that the options have only moved up 8c. The option price has moved up only 55% as much as the underlying.

This, my friends is what delta measures and is expressed as such- 55% - easy! It may also be expressed as a decimal i.e. 0.55.

Delta expressed as a plural (deltas) means the total exposure of the entire position. For example, if you have 10 US contracts (or 1000 options or 1 aussie contract) you will have 550 deltas...delta x total number of options.

OK, delta also changes depending on whether it is "in the money" (ITM), "at the money" (ATM) or "out of the money" (OTM)

As we go further ITM the delta will increase until we get to a maximum of 100% or 1.0. An option with a delta of 100% will be WAY deep in the money...and if the share moves 10c the option will move 10c

Conversely, the further out of the money we go the lower the delta with a minimum of nearly 0 when way the %$#@ OTM.

This is why if you own OTM options, although cheap to buy, the underlying will have to move a LOT before the option moves.

With put options delta is always expressed as a negative number (eg -55%). The reason is simple. If you own a put the value moves in opposite direction to the underlying, share goes up, put goes down and so on.

Implications of Delta.

If you have bought an ATM call option and the share is going up your profit will inrease at a faster and faster rate until delta reaches 100%

If the share is going down, you will be losing money, but at a slower and slower rate, until delta reaches 0, which happens to coincide with the amount of money you paid for the option.

This is the reason a straddle can be profitable but more about that later...we will also talk about "delta neutral" later.

So how fast does delta change? This is what gamma measures.....

 

[wayneL]

Gamma:

Pos says: Change in the delta of an option with respect to the change in price of its underlying security.

We have already seen that an ATM call has a delta of around 50 - 55%, and that as the share price goes up delta increases, and decreases as it goes down. (remeber puts have negative delta)

How quickly this occurs is the measurement of gamma.

Some option traders who are very mathematically inclined, like to quantify gamma. I don't think it's necessary, but I do think it's important to know when and where gamma is at is maximum and what effect it has in a relative sense.

Gamma is greatly affected by implied volatility (we talk about that later). When IV's are very low the maximum gamma is ATM. As IV inreases, maximum IV moves ITM, so when IV's are very high maximum gamma may be a long way ITM.

Why is this important? If we are buying options, either alone or as part of a spread, it helps us select the best strike price. We want high gamma in our bought options.

There is another effect of IV on gamma. Gamma decreases as IV goes up.

This means that when IV's are very low, delta will change VERY quickly, and when they are high, very slowly.

Why do we want to know this? Well as an example; if you want to construct a delta neutral strategy such as a long straddle, we want IV's as low as possible so that the high gammas will take us into profit more quickly.

Incidentally the effect of time til expiry has the same effect on gamma as IV. Longer time til expiry - same as higher volatility and visa versa.

.....I don't know whether I've managed to simplify that or not.....hmmmmmm Perhaps I should have done implied volatility first, but that's next :-/

 

[markrmau]

Thanks for the info in this thread Wayne. I was hoping that after the explanation of terms / strategies, you or someone else could provide a real life demonstration about what you are thinking as you enter/exit a trade.

Also I note that this discussion is also valid for ASX trading warrants (except you can't write your own warrants). The advantage with the trading warrants is that if anyone has a mechanical system they want to back test, the warrant OHLC data is freely available through www.float.com.au - I couldn't find historical option prices though.

 

[tech/a]

Mark.

Im sure Wayne will get to this.
There is enough to absorb as it is!

Wayne I found your

WHY this is important or WHY we do this as very informative.
I know its a bit painful but Highlighting these gems as bullet points saves scrolling and reading.

 

[wayneL]

Yes will get into some examples later, but there is a bit to get through yet.

This post is about intrinsic value, extrinsic value and implied volatility.

Intrinsic value is the amount of value an option is "in the money", simple as that. Consequently, ATM and OTM options have no intrinsic value.

For example, if you own some call options with an exersize price of $30 and the underlying is trading @ $32, you own ITM call options. If the option expires with the underlying at $32, your option is worth $2, because you can exersize that option and buy a $32 stock for $30. This part is easy because it is readily quantifiable. (sorry if this is a bit basic for some of you but it is important for my point)

Extrinsic value is the market price of an option in addition to the intrinsic value. ATM & OTM options ar ALL extrinsic value because they have no intrinsic value. If in the example above the $30 call option was trading at $3.50 when the underlying is trading at $32, then we have $2 of intrinsic value and $1.50 extrinsic value. This extrinsic value is the puzzling part for the novice.

So how is extrinsic value priced? Some more explanations, then we get into that.

Most people refer to extrinsic value as time value. I don't, because time is only part of the picture. It is true that extrinsic value "tends" to go down as time goes by, but there are anomolies in option pricing that time does not explain.

Consider this example:

We have two mythical stocks, DOG and BARK both trading at $43.50

The DOG call options are trading @ $0.95 with 2 months to run.

The BARK call options are trading @ $3.55, also with 2 months to run.

To add to the confusion, a month ago the BARK options were trading for $2.70 when the underlying was at 43.50...cheaper yet with more time left than now.

WHY?

Enter Implied Volatility:....

 

[wayneL]

So what is volatility?

Investopeadia days: A statistical measure of the tendency of a market or security to rise or fall sharply within a period of time.

We can measure volatility retrostectively by using a formula (which I can post if anyone wants) which will give us a percentage figure. This is refered to as Statistical Volatility

So if a stock is relatively stable and sedate, it's volatility may be around 15% or so. If a stock tends to bounce all over the shop very quickly it could have a statistical volatility of 50% or even much much higher.

So how does this affect option pricing?

This all goes back to extrinsic value. This extrinsic value reflects the risk taken on by the option writer (seller) that the option may expire ITM...and the risk that is may expire FAR ITM resulting in a loss for the writer. It is a "risk premium" not unlike insurance premium.

Think about it, time = risk, and volatility = risk...both together = big risk.

The more time left on the option the more chance that circumstances may push the underlying deep into the money....risk for the writer.

If you have a very volatile underlying, who knows where the hell the price will end up on expiry....risk for the writer.

Using the black-scholes option pricing model, using algebra, we can work out what volatility is priced into the option premium. But this my not reflect at all the statistical volatility of the underlying. It may be cheaper or one helluva lot more expensive than indicated by the recent past.

Why is this so? Often it is explained away as being underpriced or overpriced. But it is not this at all. It is the the perception of possible future volatility and therefore the risk to the option seller during the life of the option. This is called Implied Volatility.

Lets look at an example; WOOF is a biotech that has been plodding along in the market, not really going anywhere, and has a statistical volatilty of say, 20%. But it is known they have been working an a miracle drug promising eternal youth and the results of an extended trial are due out in 4 weeks time. When the results are released, it could mean a dramatic move to the upside or downside.

If you were an option seller, would you be selling WOOF options at supposed "fair value" of 20% volatiltiy.

NO BLOODY WAY MATE! The risk you are taking on, you might want 150% as it is likely to be a humungous gap when the news is released. We just don't know which way!

So just to repeat, Implied volatility(IV) is the markets guess of future volatilty.

There are other aspects to IV such as "Volatility Skew" and "Volatility Crush", which we will go into later.

Cheers

 

[positivecashflow]

Here is an example of Volatility Skew and Volatility Crush plotted on a graph. As wayne will probably explain, different expiry periods of options have different implied volatility levels. The difference is due to the expectations of traders and MMs that an option will move in the period specified. eg if WOOF was coming out with an announcement in 3 days that was expected to make the share price jump, then obviously the IV would be higher for options that expire near term and thus the options will increase in price (maybe due to demand).

The first image depicts a huge "volatility skew" that existed between options that expired 7-30 days away (the red line) and longer term options that expired > 90 days away (black line). Maybe traders and MMs expected the stock to move in the future rather than near term. This is all maybes at this point.

The second image depicts a drop in the IV for the longer term options (black line). This is known as volatility crush, where the IV drops and the option loses value (as wayne explained IV is priced in the options).

There are various strategies that you can employ to play volatility skews, crushes and rushes (where IV rises and your bought options increase in value even if the stock does nothing).

It is important that you manage IV effectively in your positions so that you make the most in the changes in the IV priced in options.

Back to you wayne.

 

[wayneL]

It is important that you manage IV effectively in your positions so that you make the most in the changes in the IV priced in options.

That deserves to be in bold!

It is important that you manage IV effectively in your positions so that you make the most in the changes in the IV priced in options.

IV can be a huge trap for the unwary and a great opportunity if you know what to do with it.

Good stuff Pos!

 

[wayneL]

Vega (sometimes known as Omega) is the effect on option prices from changes in Implied Volatility.

Like Gamma, I don't bother to quantify Vega (you can if you have a superhuman mathematical brain). But like Gamma it is necessary to know where vega has the greatest effect.

Vega has the greatest effect when At The Money and diminishes the further you get away from the money.

So what this means is, if you have bought an ATM option at high IV's ( which you want to avoid like the pox, unless as part of a spread), you're praying that IV's don't decrease, because it's gonna hurt. It will hurt less so if your option is away from the money. Conversely if you bought an option at low IV's, you don't care if IV goes up because it's to your benefit.

Example: MEOW is trading at $25 with option IV's @50%, and for some inexplicable reason, you buy the $20 call for $5.50, the $25 call for $2.15, and the $30 call for $0.65

For some equally inexplicable reason IV's fall to 40% during the day, and the price hasn't changed. This is what happens:

$20 call goes from $5.50 to $5.35, you lose 15c
$25 call goes from $2.15 to $1.75, you lose 40c
$30 call goes from $0.60 to $0.35, you lose 25c

So we can see here that vega is greatest ATM.

It's clear why we want to know this, If we're buying options we want to buy at lower end of an options IV' range so that vega will work in our favour ...and of course the opposite if we're writing options.

One more point, vega decreases the nearer we get to expiry.

One more greek to go... Theta

 

[seaurchin]

hi wayneL & tech /a and other traders...thanks for the interesting information on options etc.
I have only been paper trading and was successfull inside 2weeks.
so i went in and bought bhp calls monday sold tues. 20% gross profit.

However, I have good relationship with broker and trust him.

My question is I have only the use of ASX.site which is 20 minutes delay or so
Normally as you know you have m/depth to help see the supply demand of stocks instantly...ASX options I see open interest and volume only.

Is there a site which can have this info. faster and market depth.
thanks for your help.