RichKid
PlanYourTrade > TradeYourPlan
- Joined
- 18 June 2004
- Posts
- 3,031
- Reactions
- 5
Hi folks,
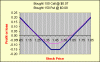
Been following some of WayneL's posts and been doing some basic reading on options. I'm currently new to options so I'm looking at a simple strategy to get started while reducing risk. I've found the strangle to be attractive at this stage of the market as I expect some further movement in either direction of at least 100 points in the next 3 months or so and I can only allocate a small amount of my capital (ie strangle is cheaper than a straddle but riskier).
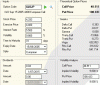
So here is a screen shot of some option prices I've been looking at (the XJOFF is just for comparison purposes) from the ASX site as of about 10 minutes ago. The top and bottom options are the ones that I am looking at for the strangle. My basic question to anyone who'd like to help is why is there such a difference between the theoretical and market (mm) price and is it too expensive in that sense? Unlike shares I know that I'm buying from other investors directly but here I'm not sure if it's just a numbers conjuring trick. How do you pros decide what to pay for an option?
As for my strategy does anyone recommend another combination, this is a learning exercise so don't think it's a trade recommendation as I won't buy on your advice. You can suggest your own strangle combination if you like and we can debate it to draw out the theoretical & pricing issues. With strangles do you buy any combination of otm puts and calls eitherside of the current price or do you buy them at equal strike distances away from the current price (eg put strike approx 100 ticks away from current price and call approx 100 ticks away from current price??). I've also posted some info from the ASX site about strangles (next post).
Real times prices for the options at the time were (average of spread):
XJOI5 39c
XJOFF (no spread)
XJOJP 33c
Been following some of WayneL's posts and been doing some basic reading on options. I'm currently new to options so I'm looking at a simple strategy to get started while reducing risk. I've found the strangle to be attractive at this stage of the market as I expect some further movement in either direction of at least 100 points in the next 3 months or so and I can only allocate a small amount of my capital (ie strangle is cheaper than a straddle but riskier).
So here is a screen shot of some option prices I've been looking at (the XJOFF is just for comparison purposes) from the ASX site as of about 10 minutes ago. The top and bottom options are the ones that I am looking at for the strangle. My basic question to anyone who'd like to help is why is there such a difference between the theoretical and market (mm) price and is it too expensive in that sense? Unlike shares I know that I'm buying from other investors directly but here I'm not sure if it's just a numbers conjuring trick. How do you pros decide what to pay for an option?
As for my strategy does anyone recommend another combination, this is a learning exercise so don't think it's a trade recommendation as I won't buy on your advice. You can suggest your own strangle combination if you like and we can debate it to draw out the theoretical & pricing issues. With strangles do you buy any combination of otm puts and calls eitherside of the current price or do you buy them at equal strike distances away from the current price (eg put strike approx 100 ticks away from current price and call approx 100 ticks away from current price??). I've also posted some info from the ASX site about strangles (next post).
Real times prices for the options at the time were (average of spread):
XJOI5 39c
XJOFF (no spread)
XJOJP 33c