- Joined
- 18 September 2008
- Posts
- 4,041
- Reactions
- 1,185
Q5: 35 cm^2
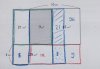
For those who are having difficulty working out the solution without resorting to computing interim fractions or using algebra, this is how Number 3 is worked out.

You can easily calculate the missing rectangle in the top left hand corner (delineated in red) as its sides are obviously 1 X 5. It has a width 1 because its width is the difference between the widths of the rectangle immediately to its right (4) and that below it (5). It has a height of 5 because it has the same height as the rectangle beside it, which must be 20 divided by 4.
If you then add the areas of this new rectangle with those of the rectangle to its left and the rectangle below it, you get a new combination rectangle of 5 + 20 + 14 or 39cm2. This combination rectangle is exactly half the area of the large rectangle on the right (78cms) and as it shares the same height, its width then must be half that of the bigger rectangle. But we know the combination rectangle has a width of 5, therefore the bigger one must have a width of 10cm, which is the answer we are looking for.
According to the source article, the reason these puzzles are to be solved without use of fractions or algebra, basically with just the knowledge that the area of a rectangle equals its width by height, is that these are problems set for Japanese school kids who haven't yet got to the stage where they have learned about algebra or fractions.