- Joined
- 3 June 2013
- Posts
- 457
- Reactions
- 53
Re: Stop Loss is not always your friend....
Apologies for being late to the party, I wanted to give this some proper research and time was short over the last week.
My intention was to run a few backtest that clearly show that stop losses are not your friend in a fundamentally oriented, long term portfolio. A little bit of bias on my side. I remember running some tests a long time ago that didn't inspire me, I thought I'll do it properly this time.
To start off with, I establish a benchmark - which is a return I would get by investing into all stocks in my universe. I set a period of 5 years, and it happened to give me a return of 68.41%.
Then, I select a strategy that beats the benchmark. Let's use the old and tried Net Assets. We buy when P/B < 0.7, we sell when P/B > 2. Position Size = 2%, brokerage = $30. Here's how it compares to the benchmark:

Higher return and more winners, but also more big losers. Nothing controversial so far. Let's now add stop losses to this winning strategy. I'll backtest on stop losses at 5%, 10% and 20%. Once stopped, share will not be bought again the next 365 days. Here are the results:
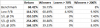
Equity Curve:

Hold on, that's not right, not the result I was expecting. Perhaps it just happened to work with this strategy, let's try a low PE strategy. Equity curve:
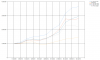
An identical result to the P/B strategy - stop losses improve the result, and the tighter the stop loss the better.
How about trailing stop losses? Not so good:

I am limited to 5 attachments, to be continued in next post.
Apologies for being late to the party, I wanted to give this some proper research and time was short over the last week.
My intention was to run a few backtest that clearly show that stop losses are not your friend in a fundamentally oriented, long term portfolio. A little bit of bias on my side. I remember running some tests a long time ago that didn't inspire me, I thought I'll do it properly this time.
To start off with, I establish a benchmark - which is a return I would get by investing into all stocks in my universe. I set a period of 5 years, and it happened to give me a return of 68.41%.
Then, I select a strategy that beats the benchmark. Let's use the old and tried Net Assets. We buy when P/B < 0.7, we sell when P/B > 2. Position Size = 2%, brokerage = $30. Here's how it compares to the benchmark:
Higher return and more winners, but also more big losers. Nothing controversial so far. Let's now add stop losses to this winning strategy. I'll backtest on stop losses at 5%, 10% and 20%. Once stopped, share will not be bought again the next 365 days. Here are the results:
Equity Curve:

Hold on, that's not right, not the result I was expecting. Perhaps it just happened to work with this strategy, let's try a low PE strategy. Equity curve:

An identical result to the P/B strategy - stop losses improve the result, and the tighter the stop loss the better.
How about trailing stop losses? Not so good:
I am limited to 5 attachments, to be continued in next post.


