- Joined
- 21 August 2008
- Posts
- 2,832
- Reactions
- 8,776
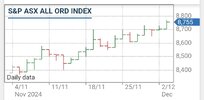
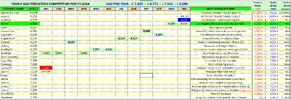
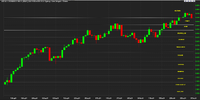
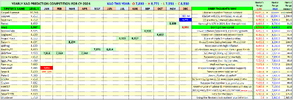
Oh @farmerge old mate, I see you have put on your old glasses from earlier in the year and posted in the wrong thread. Get rid of them, the new glasses have worked a treat all year.@debtfree Oh wise and benevolent one. My musings on FMG, WES, WBC and STX, though somewhat a tad late, have been completed for the month.
I'm updating things this morning, so I'll chase the posts down. Thanks mate.